What can business problem solvers learn from physics?

by Dr James Mills

View PDF version

Novelty lies at the heart of creativity and innovation; however, the building blocks of new innovations are often found in existing bodies of knowledge. The creative aspect of innovation is found in the application of existing ideas in different contexts. As Mark Twain put it, ‘There is no such thing as a new idea. It is impossible. We simply take a lot of old ideas and put them into a sort of mental kaleidoscope’ (Twain 1907). In recognition of this, organisations are increasingly encouraging multi-disciplinary teams to promote the rediscovery of existing ideas in new settings (Fleming 2004, Feitler 2014, Uzzi et. al. 2013).

With increasing awareness of the advantages associated with breadth of training and experience, business problems are increasingly being tackled by teams that possess ‘unconventional’ skill sets. For example, a 2016 report by the American Institute of Physics found that, outside of academia, employment within the business sector has become the third most common post-doctoral career path for physicists (Pold & Mulvey 2016).

In a research context, and within technical teams where industry specific expertise is advantageous, the benefit of having an interdisciplinary workforce is self-evident. However, in non-technical fields, the advantages derived from drawing upon a range of training and experience are less clear cut. In this article we make the case for tackling business problems from novel perspectives by exploring what business problem solvers can learn from physics.

Problem solving by analogy

In physics, it is possible for an exact correspondence to exist between apparently unconnected problems when the underlying ‘equations of motion’ governing the systems in question are the same. This allows physics problem solvers to draw valuable insights about a system they may have never observed, by mapping the problem onto a familiar system with known behaviour.

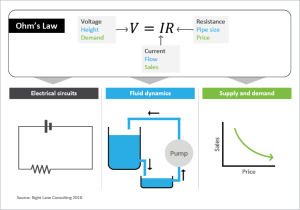
Ohm’s Law: An illustrative example

Electricity and fluid dynamics are examples of two apparently unrelated physical phenomena which are nevertheless connected by a powerful analogy. Because many people have difficulty visualising the forces at play in an electrical circuit, a common conceptual aid is to map this system onto a more familiar one, water flowing through a pipe. This correspondence is shown graphically in Exhibit 1. The height of the reservoir plays the role of voltage, the resistance is related to the diameter of the pipe, and the rate at which the water flows through the system is equivalent to the electrical current. This analogy allows us to draw conclusions about what will happen to the electrical current as we alter the voltage or resistance based on our understanding of the way in which water flows.

This approach works because, to a good approximation, the equations which describe the flow of electricity are equivalent to those that describe the movement of a fluid. For electrical systems this equation is known as Ohm’s Law and states that the voltage (V), electrical current (I), and resistance (R) obey the relationship V = IR. The analogy between electrical circuits and fluid dynamics is so powerful that it has become ingrained within the terminology of the field; we note, for example, that the flow of electricity is referred to as a ‘current’.

Exhibit 1: Analogies can powerfully aid comprehension

Exhibit 1: Analogies can powerfully aid comprehension

Analogous business situations

Unfortunately, business problems rarely permit precise mathematical representation. In this context, is it still possible to identify systems which behave similarly, and if so, is such a grouping useful? The answer to these questions is an emphatic yes. Even when it is not possible to write down a precise mathematical description of the business situation, considering the fundamental forces at work can allow us to draw valuable insights.

Returning to the Ohm’s Law example discussed previously we can see that the fundamental components of this system are a driving force, a resistance, and a rate of flow. There are many business situations in which these same components arise. Take for example, the sales of a particular widget, which are driven by its intrinsic value proposition, and are resisted by the price charged. A common practice is to describe this situation using supply and demand curves such as that as shown in Exhibit 1. What is less apparent, is that drawing these curves is equivalent to stating that the relationship between demand, price and the intrinsic value of the product is given by Ohm’s Law.

So far we have assumed perfect economic efficiency; every individual who will receive greater value from the widget than the price charged becomes a customer. In reality, many other factors may impact sales, such as marketing activities which may increase the perceived value proposition and inefficiencies within distribution channels, which act to reduce the number of potential customers that are reached. We can extend the analogy to include these factors as additional voltage sources or resistances.

Making use of the analogy

The observation that a business situation behaves in a manner analogous to Ohm’s Law does not in itself tell us anything new about the business problem we are trying to solve. So how can we draw upon this analogy to derive fresh insights about the business situation?

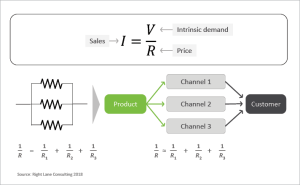
To illustrate the utility of problem solving by analogy, consider a situation in which a product is distributed via multiple channels, with the cost to consumers varying between the channels. We want to determine how a change in the cost of one channel will affect the total sales.

Again, we identify this as an Ohm’s Law problem with demand, price and sales playing the role of voltage, resistance and current respectively. Since each of the channels act independently of one another, this situation maps to a system of resistors in parallel, which is shown diagrammatically in Exhibit 2. This problem has a well know solution in physics: the total resistance is found by summing the inverses of the individual resistances. By analogy, we are able to say that the total ‘resistance’ across all channels is given by the sum of the inverses of the individual ‘channel resistances’, their respective prices. Inserting this result into Ohm’s Law allows us to predict how changes in the channel costs will impact the total sales.

Exhibit 2: Problem solving by analogy

Exhibit 2: Problem solving by analogy

Of course, this is only one way of approaching this problem and is not necessarily the best approach. We highlight this example because it is emblematic of the way in which bringing a variety of training and experience to bear can uncover novel and insightful ways of thinking about business problems.

Cultivating a broad range of training and experience allows business problems to be approached from multiple perspectives. This helps to eliminate erroneous conclusions, which are unlikely to result simultaneously from independent logical processes, and permits the development of mutually supportive analyses.

References

Feitler, D 2014, ‘The Case for Team Diversity Gets Even Better’, Harvard Business Review, March.

Fleming, L 2004, ‘Perfecting Cross-Pollination’, Harvard Business Review, September.

Pold, J & Mulvey, P 2016, ‘Physics Doctorates Initial Employment’, American Institute of Physics, June.

Twain, M 1907, Mark Twain’s Own Autobiography: The Chapters from the North American Review, University of Wisconsin Press.

Uzzi, B, Mukherjee, S, Stringer, M & Jones, B 2013, ‘Atypical Combinations and Scientific Impact’, Science, October.

For more information contact James Mills at james.mills@rightlane.com.au

© 2018 Right Lane Consulting